Integration of the "red line" in order to calculate the second high school kinematic equation
To be able to find the integral we must first find the formula for the read line (velocity graph).
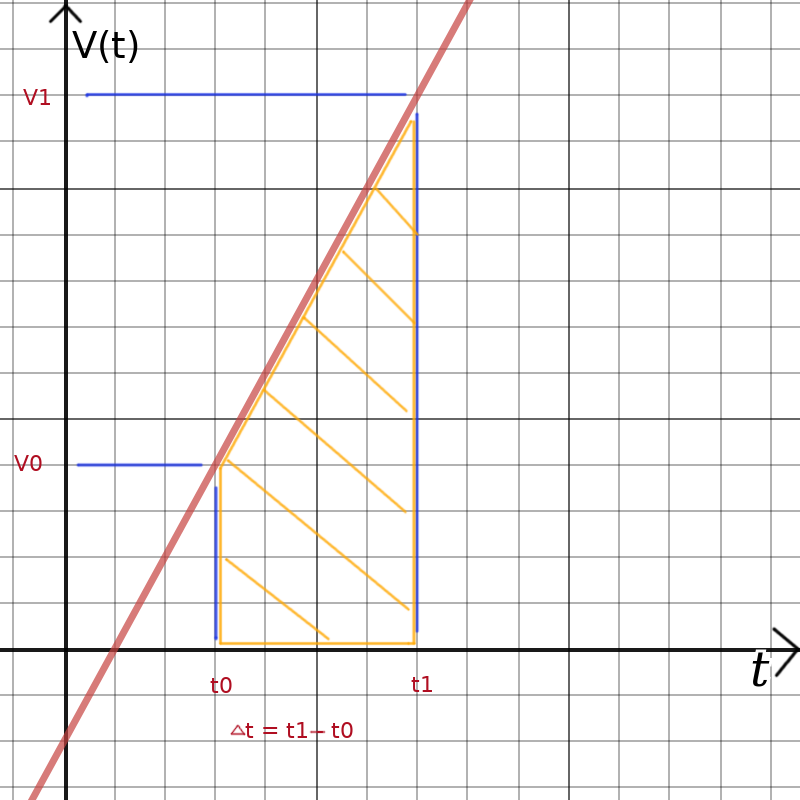
The assumption under which the high school equation is valid, is: The velocity increases linear from V0 to V1 over the time period Δt.
Δt = t1 - t0
The slope m of the red line is:
V1 - V0
m = ---------
t1 - t0
The general formula of a line is: y = m * x + b. In our case we have t on the x-axis and v(t) on the y-axis.
The formula for the velocity over time for this specific line is therefore:
V1 - V0
v(t) = -------- * t + b
t1 - t0
b is the y-intersect:
V1 - V0
b = V1 - ---------- * t1
t1 - t0
Thus the general formula for this red line, v(t), is:
V1 - V0 V1 - V0
v(t) = -------- * t + V1 - --------- * t1
t1 - t0 t1 - t0
Now we have to find the integral of v(t) for the section from t=t0 to t=t1.
Let's abbreviate the formula a bit by introducing the constant m for the slope and b for the y-intersect:
v(t) = m * t + b
The integral of v(t) is:
∫v(t)∂t = ½ * m * t2 + b * t
The integral from t=t0 to t=t1 is therefore:
½ * m * t12 + b * t1 - ( ½ * m * t02 + b * t0)
We put the values for b and m back into the equation and we get:
1 V1 - V0 V1 - V0 ( 1 V1 - V0 V1 - V0 )
- ------- t12 + V1t1 - ------- t12 - ( - -------- t02 + V1t0 - ------- t1t0)
2 t1 - t0 t1 - t0 ( 2 t1 - t0 t1 - t0 )
this is equal to:
1 V1 - V0 1 V1 - V0 V1 - V0
- -- ------- t12 + V1t1 - -- ------- t02 - V1t0 + -------- t1t0
2 t1 - t0 2 t1 - t0 t1 - t0
since our aim is to eventually replace t1 - t0 with Δt we rewrite the equation like this:
1 V1 - V0 V1 - V0
- -- ------- (t12 + t02) + V1 (t1 - t0) + -------- t1t0
2 t1 - t0 t1 - t0
With t12 + t02 = (t1 - t0)2 + 2t1t0 we can re-write the equation as follows:
V1 - V0
------- (- ½(t1 - t0)2 - ½ 2t1t0 + t1t0 ) + V1 (t1 - t0)
t1 - t0
this is equal to (replace t1 - t0 with Δt):
V1 - V0
- ------- Δt + V1 Δt
2
this is equal to:
½ (V0 + V1) Δt
and that is the solution of the integral ∫v(t)∂t with v(t) being a line starting at V0 and ending at V1 over the time period Δt.
